Praticando Matemática: Como Resolver Questões de Diferenciação e Integração

Conteúdo

Introdução

Este guia oferece uma abordagem prática e didática de como resolver questões de diferenciação e integração. A diferenciação e a integração são pilares do cálculo, com aplicações em diversas áreas, como Física, Engenharia, Economia e Medicina. Para estudantes, dominar esses conceitos não apenas garante bons resultados em provas, mas também desenvolve habilidades essenciais de raciocínio lógico e resolução de problemas.

Com exemplos e exercícios comentados, você aprenderá desde as regras básicas até estratégias para resolver problemas mais complexos.

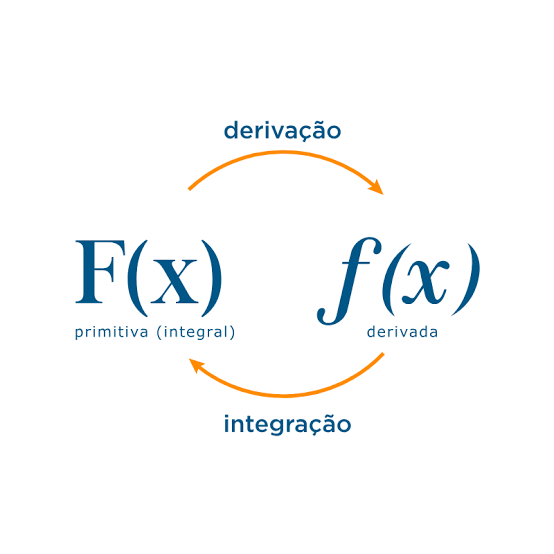
O que é Diferenciação e Integração?
Diferenciação
A diferenciação mede a taxa de variação de uma função, ou seja, como uma variável muda em relação a outra.

Exemplo:
Se $f(x) = x^2$ , sua derivada $f'(x)$ representa como $f(x)$ cresce à medida que $x$ aumenta.

Fórmula básica:

$f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$

a) Integração

A integração calcula a área acumulada sob uma curva ou a soma de infinitos elementos infinitesimais.

Exemplo:
A integral de $f(x) = x^2$ entre $x = 0$ e $x = 1$ mede a área abaixo dessa curva.

Fórmula básica da integral definida:

$\int_a^b f(x) , dx$

Regras Fundamentais da Diferenciação
Derivada de uma constante: $\frac{d}{dx}(c) = 0$
Derivada de $x^n$ : $\frac{d}{dx}(x^n) = n \cdot x^{n-1}$
Regra do Produto: $\frac{d}{dx}[f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x) \cdot g'(x)$
Regra do Quociente: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{g(x)^2}$
Regra da Cadeia: $\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)$
Exemplo Resolvido:
Questão: Derive $f(x) = 3x^3 - 5x + 7$ .

Resolução:

Derivada do primeiro termo: $\frac{d}{dx}(3x^3) = 9x^2$
Derivada do segundo termo: $\frac{d}{dx}(-5x) = -5$
Derivada do terceiro termo: $\frac{d}{dx}(7) = 0$
Portanto, $f'(x) = 9x^2 - 5$ .

Regras Fundamentais da Integração
Integral de uma constante: $\int c , dx = c \cdot x + C$
Integral de $x^n$ : $\int x^n , dx = \frac{x^{n+1}}{n+1} + C$ , para $n \neq -1$
Integral de uma soma: $\int [f(x) + g(x)] , dx = \int f(x) , dx + \int g(x) , dx$
Exemplo Resolvido:
Questão: Calcule $\int (2x^2 - 4x + 5) , dx$ .

Resolução:

Integral do primeiro termo: $\int 2x^2 , dx = \frac{2x^3}{3}$
Integral do segundo termo: $\int -4x , dx = -2x^2$
Integral do terceiro termo: $\int 5 , dx = 5x$
Portanto, $\int (2x^2 - 4x + 5) , dx = \frac{2x^3}{3} - 2x^2 + 5x + C$ .

Aplicações de Diferenciação e Integração
a) Velocidade e Aceleração
A derivada da posição em função do tempo, $s(t)$ , dá a velocidade: $v(t) = s'(t)$ .
A derivada da velocidade dá a aceleração: $a(t) = v'(t)$ .

b) Cálculo de Áreas

Para encontrar a área entre uma curva $f(x)$ e o eixo $x$ , usa-se a integral definida:
$\text{Area} = \int_a^b f(x) , dx$ .

c) Otimização

Problemas de maximização e minimização envolvem encontrar pontos críticos de uma função. Resolva $f'(x) = 0$ para identificar máximos ou mínimos locais.

Questões Comuns de Provas
Questão 1: Velocidade e Aceleração
Enunciado:
A posição de um objeto é dada por $s(t) = t^3 - 6t^2 + 9t$ . Determine a velocidade e a aceleração no instante $t = 2$ .

Resolução:

Velocidade: $v(t) = s'(t) = 3t^2 - 12t + 9$ .
Substituindo $t = 2$ : $v(2) = 3(2^2) - 12(2) + 9 = -3$ .

Aceleração: $a(t) = v'(t) = 6t - 12$ .
Substituindo $t = 2$ : $a(2) = 6(2) - 12 = 0$ .

Questão 2: Área entre Curvas
Enunciado:
Calcule a área entre $f(x) = x^2$ e $g(x) = x$ no intervalo $[0, 1]$ .

Resolução:
Área: $\int_0^1 [g(x) - f(x)] , dx = \int_0^1 (x - x^2) , dx$ .

Integral:
$\int x , dx = \frac{x^2}{2}$ , $\int x^2 , dx = \frac{x^3}{3}$ .

Substituindo os limites:
$\left[\frac{x^2}{2} - \frac{x^3}{3}\right]_0^1 = \frac{1}{2} - \frac{1}{3} = \frac{1}{6}$ .

Conclusão

Diferenciação e integração são ferramentas poderosas, essenciais para resolver problemas práticos e teóricos. Praticar com questões contextualizadas ajuda a fixar os conceitos e aumenta sua confiança para enfrentar provas e desafios reais.

Com dedicação, você estará pronto para dominar o cálculo e usá-lo como uma habilidade indispensável em diversas áreas do conhecimento.

parteOm

Praticando Matemática: Como Resolver Questões de Diferenciação e Integração

— by

Introdução

a) Integração

b) Cálculo de Áreas

c) Otimização

Conclusão

Deixe um comentário Cancelar resposta

Social

Pages

Praticando Matemática: Como Resolver Questões de Diferenciação e Integração

— by

Introdução

a) Integração

b) Cálculo de Áreas

c) Otimização

Conclusão

Compartilhe isso:

Mais Vistos

Deixe um comentário Cancelar resposta