Funções e Gráficos para Vestibular Medicina: Tópicos Essenciais

Conteúdo

Introdução

Dominar o conceito de Funções e Gráficos para Vestibular Medicina é fundamental para obter sucesso nas questões de matemática dos vestibulares, especialmente onde o raciocínio lógico e matemático é exigido em alto nível. Neste guia, abordaremos os principais tipos de funções e suas representações gráficas, além de oferecer dicas práticas para resolver questões de vestibulares com segurança.

O que é uma Função?

Uma função é uma relação matemática que associa elementos de dois conjuntos, onde cada elemento de um conjunto (domínio) tem um único correspondente no outro conjunto (imagem). Em termos formais, uma função é expressa como $f(x)$ , onde para cada valor de $x$ , há um valor correspondente de $y$ tal que $y=f(x)$ .

Um exemplo simples de função é a função linear $f(x) = 2x + 3$ . Para cada valor de $x$ , é possível encontrar um valor correspondente de $y$ , o que torna possível construir um gráfico que represente essa relação.

Tipos de Funções Mais Comuns no Vestibular

1. Função Linear

Uma função linear é expressa na forma $f(x) = ax + b$ , onde $a$ é o coeficiente angular (indica a inclinação da reta) e $b$ é o coeficiente linear (indica onde a reta intercepta o eixo $y$ ).

Exemplo prático:

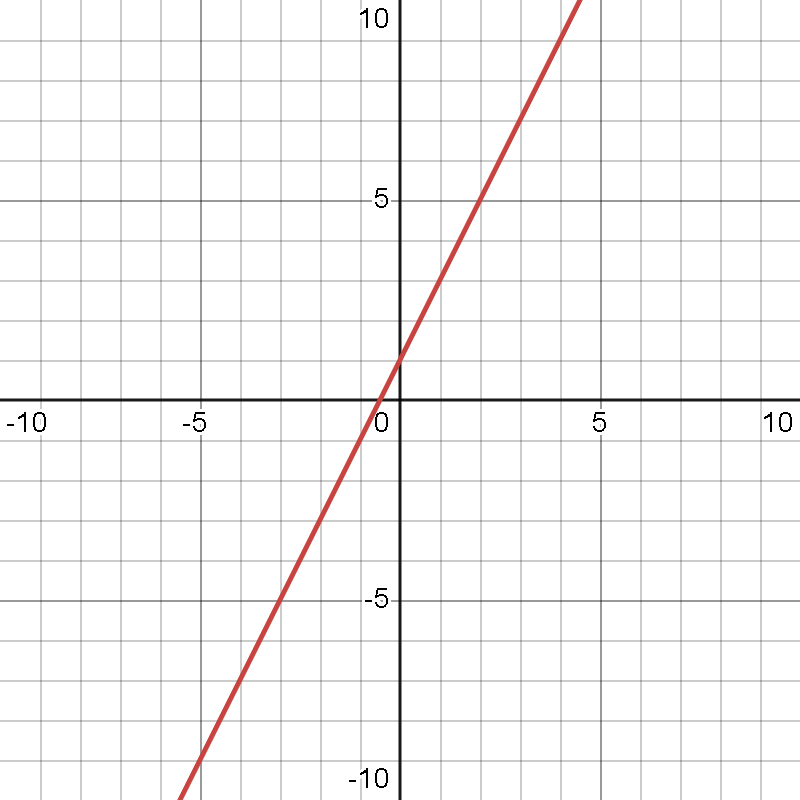
Para a função $f(x) = 2x + 1$ , o gráfico será uma reta com inclinação positiva. A cada unidade que $x$ aumenta, o valor de $y$ aumenta em duas unidades.

2. Função Quadrática

As funções quadráticas são representadas por $f(x) = ax^2 + bx + c$ . O gráfico de uma função quadrática é uma parábola. Se o valor de $a$ for positivo, a parábola será aberta para cima, e se $a$ for negativo, será aberta para baixo.

Exemplo prático:

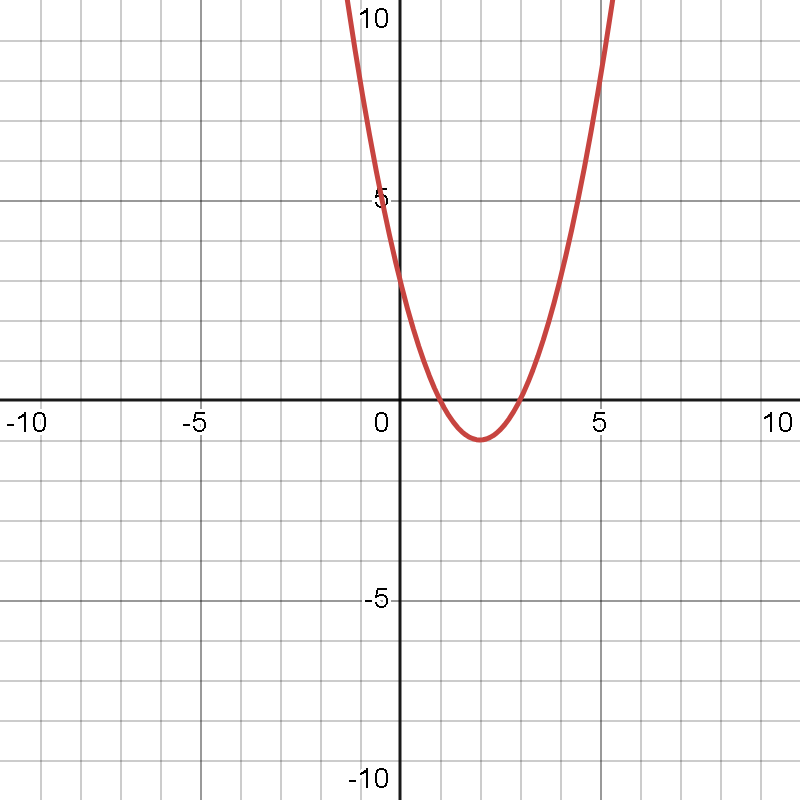
A função $f(x) = x^2 - 4x + 3$ tem como gráfico uma parábola que intercepta o eixo $x$ em $x = 1$ e $x = 3$ , e o vértice da parábola estará no ponto $(2,-1)$ .

3. Função Exponencial

Funções exponenciais têm a forma $f(x) = a^x, onde[latex]a>0$ . Essas funções crescem ou decrescem rapidamente, dependendo do valor de $a$ .

Exemplo prático:

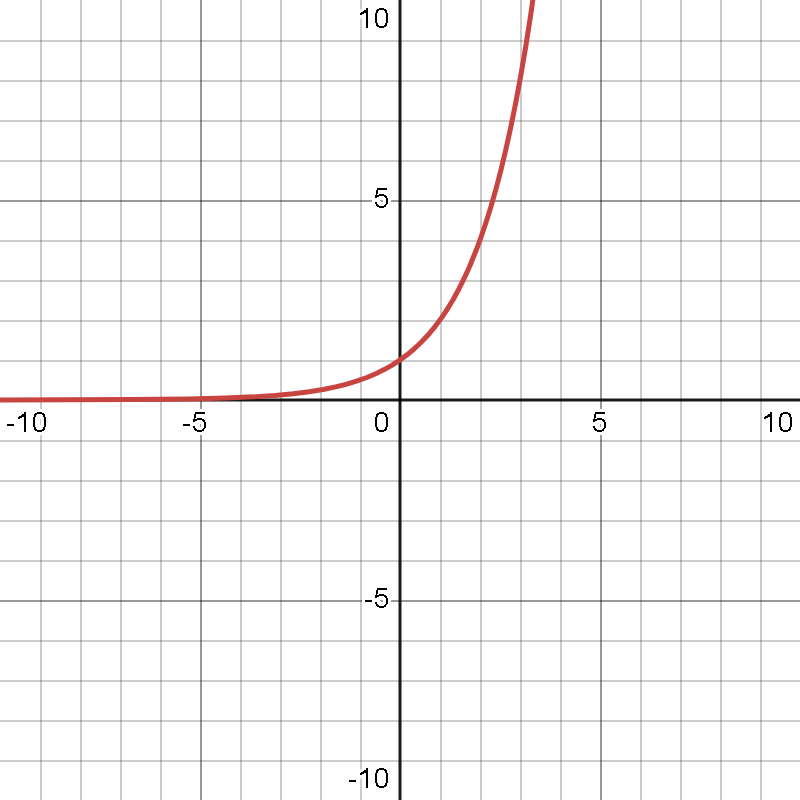
Para $f(x) = 2^x$ , à medida que $x$ aumenta, o valor de $y$ cresce exponencialmente. Quando $x$ é negativo, o valor de $y$ se aproxima de zero, mas nunca o toca.

4. Função Logarítmica

A função logarítmica é a inversa da função exponencial e é dada por $f(x) = \log_a(x)$ , onde $a$ é a base do logaritmo.

Exemplo prático:

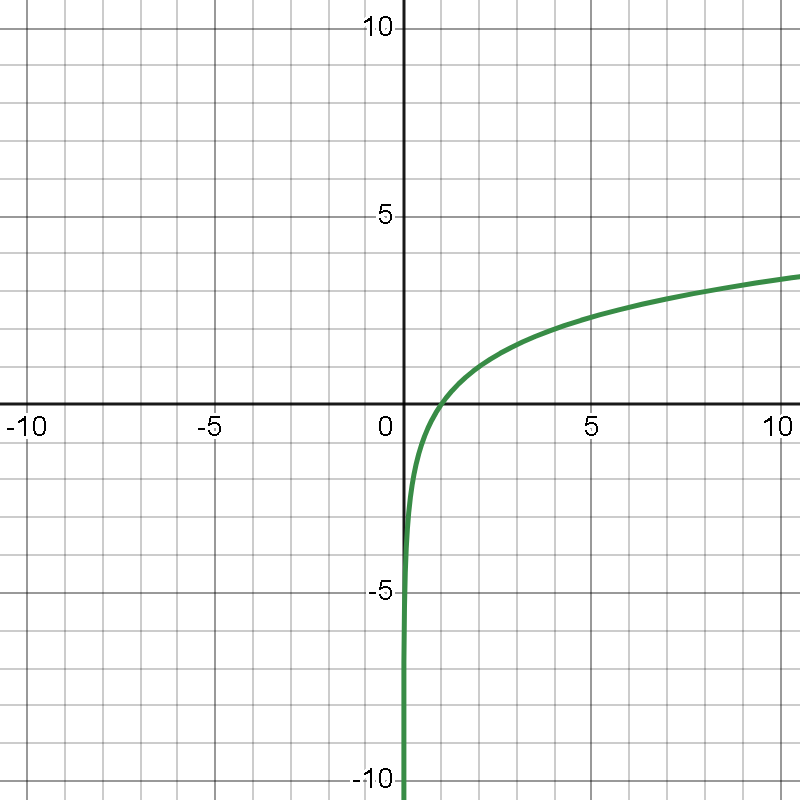
O gráfico de $f(x) = \log_2(x)$ é crescente, mas de forma mais lenta em comparação à função exponencial, e passa por $(1,0)$ , pois $\log_2(1) = 0$ .

Como Resolver Questões de Funções e Gráficos no Vestibular

Resolver questões de funções e gráficos requer boa interpretação da equação e do gráfico fornecido. Algumas dicas para lidar com esses problemas são:

Identifique o tipo de função: Saber se a função é linear, quadrática, exponencial ou logarítmica ajuda a prever a forma do gráfico.
Use os interceptos: Os pontos onde a função intercepta os eixos $x$ e $y$ são fundamentais para traçar o gráfico.
Observe o comportamento da função: Para funções quadráticas, veja se a parábola abre para cima ou para baixo. Para funções exponenciais, veja se o crescimento é acelerado ou se aproxima de zero.

Dicas para Estudar Funções e Gráficos

Pratique a Resolução de Questões: Resolver exercícios é a melhor forma de entender as diferenças entre os tipos de funções e como elas se comportam graficamente.
Construa Gráficos Manualmente: Traçar gráficos à mão ajuda a entender como os coeficientes $a$ , $b$ e $c$ influenciam na forma do gráfico.
Estude as Fórmulas: Memorize as fórmulas das principais funções e como derivá-las ou integrá-las, pois são frequentemente solicitadas em questões mais complexas.

Exercício Prático

Vamos resolver uma questão envolvendo a função quadrática $f(x) = x^2 - 5x + 6$ .

Primeiro, determinamos os zeros da função, resolvendo a equação $x^2 - 5x + 6 = 0$ . Fatorando a equação, temos:

$f(x) = (x - 2)(x - 3) = 0$

Logo, os valores de $x$ que tornam $f(x) = 0$ são $x = 2$ e $x = 3$ , que são as raízes da função e os pontos onde o gráfico intercepta o eixo $x$ .

ARTIGOS:

parteOm

Funções e Gráficos para Vestibular Medicina: Tópicos Essenciais

— by

Introdução

O que é uma Função?